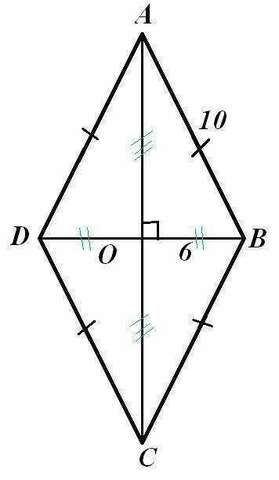
Чертеж - во вложении.
Пусть дан ромб АВСD со стороной АВ=10см, диагональ DB=12см.
Диагонали ромба точкой пересечения делятся пополам. Поэтому АО=ОС и OD=OB=6см.
Диагональ ромба взаимно перпендикулярны. Поэтому Δ АОВ - прямоугольный. По теореме Пифагора АО² = АВ² - ОВ² = 100-36 = 64.
Значит, АО = 8см, а АС = 2·8 = 16см.
Площадь ромба равна половине произведения диагоналей.
S = ½·АС·BD=½·16·12 = 96см².
Ответ: 96см².