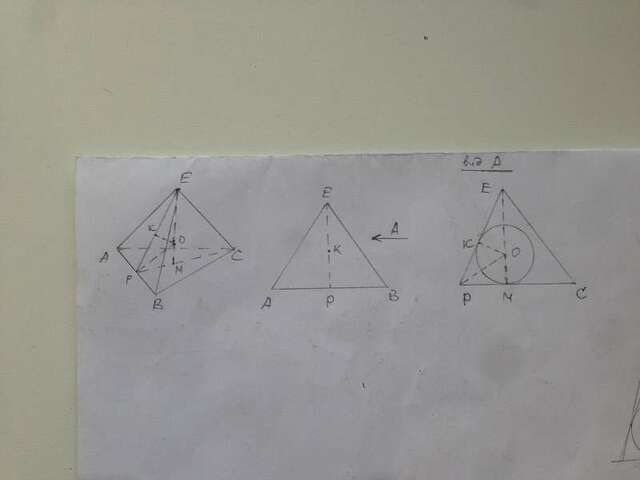
Сфера вписана в правильную пирамиду, значит основание высоты лежит в центре вписанной в основание окружности. r₀=ВМ.
Радиус сферы - отрезки КО и МО. r₁=КО=МО.
Прямоугольные треугольники РКО и РМО равны, так как КО=МО и РО - общая сторона.
По условию РК - радиус вписанной в боковую грань окружности.
В тр-ках АВЕ и АВС радиусы вписанных окружностей равны, АВ - общая сторона, оба треугольника равнобедренные, значит треугольники равны.
В пирамиде ЕАВС боковые грани равны основанию, следовательно их площади равны, значит площадь полной поверхности пирамиды:
Sполн=4Sосн=4·6.2=24.8 (ед²) - это ответ.