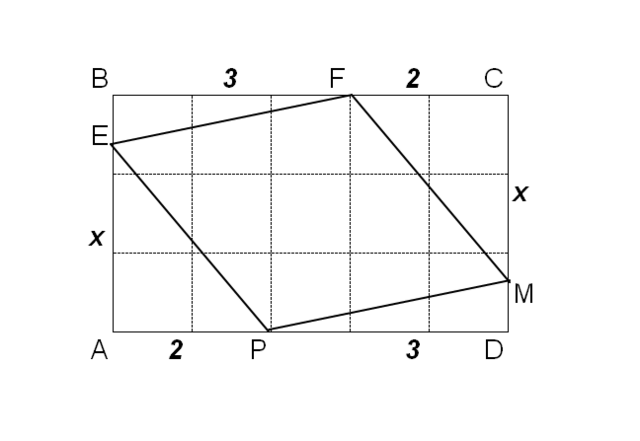
Из соображений симметрии FC=AP=2 и AE=CM=x (неизвестная длина)
Ромб - четырехугольник, у которого все стороны равны:
PE=EF=FM=MP (гипотенузы треугольников PAE, EBF, FCM, MDP)
По теореме Пифагора
2^2+x^2=(3-x)^2+3^2
4+x^2=9-6x+x^2+9
6x=14
x=7/3
Нашли все отрезки:
AE=CM=7/3
EB=MD=2/3
Далее находим сумму площадей всех треугольников PAE, EBF, FCM, MDP
St=(1/2)*2*(7/3)+(1/2)*3*(2/3)+(1/2)*2*(7/3)+(1/2)*3*(2/3)=7/3+1+7/3+1=20/3
Площадь прямоугольника S=5*3=15
Площадь ромба s=S-St=15-20/3=25/3
Отношение площадей прямоугольника и ромба
S/s=15/(25/3)=9/5
Ответ: отношение площадей прямоугольника и ромба = 9/5