1.какое из утверждений верно относительно треугольника со сторонами 15, 9, 12. 2....

Question

1.какое из утверждений верно относительно треугольника со сторонами 15, 9, 12. 2. окружность с центром О, вписанная в равнобедренный треугольник ABC с основанием AC, касается стороны BC в точке K, причем CK : BK = 5 : 8. найдите площадь треугольника, если его периметр равен 72. прошу с кратким, объяснением.

Answer 1

1. Он прямоугольный, т.к. квадрат одной стороны равен сумме квадратов двух других.

 

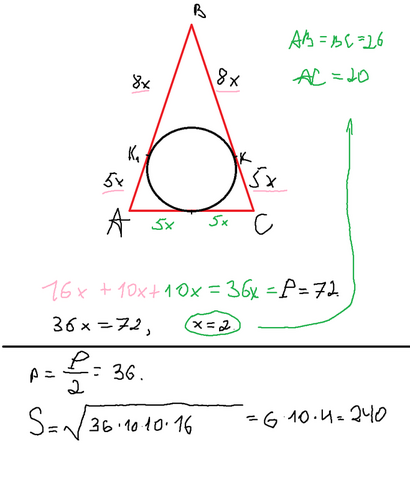
2. Т.к. АВС равнобедренный, то, очевидно, точка касания с другим бедром - АВ - будет делить его в таком же отношении. Далее вводим коэффициент пропорциональности х.

Теперь смотрим на основание. По теореме об окружности, вписанной в угол, мы имеем, что расстояния от вершины угла (в данном случае точки А и С со вписанной окружностью) до точек касания равны. Так, получается, что основание равно 10х.

 

Складываем все стороны и вычисляем х через известный периметр. Из этого находим все стороны треугольника.

Если все стороны известны, то площадь можно найти по формуле Герона.

---