Сборник задач по физике под редакцией Савченко. задание 1.3.30* звучит так (дословно)...

Question

148 просмотров

Сборник задач по физике под редакцией Савченко. задание 1.3.30* звучит так (дословно)

Снаряд вылетает из пушки со скоростью V под углом α к горизонту.
Какое время снаряд приближается к пушке ?

рассмотреть нужно достаточно большие углы (около 90 градусов) и из всей траектории только ту часть когда падающий снаряд ПРИБЛИЖАЕТСЯ к пушке.

1.считаю что задача красивая и должна остаться на сайте решенной.
2.решить задачу не могу потому что я автор вопроса )))

Физика IUV_zn (219k баллов) 29 Апр, 18 | 148 просмотров

Дан 1 ответ

Правильный ответ

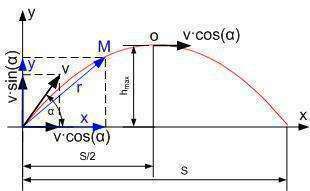
Если пренебречь сопротивлением воздуха и считать снаряд материальной точкой, то задача о движении снаряда, выпущенного из пушки под углом α к горизонту с начальной скоростью v, сводится к известной задаче о движении тела, брошенного под углом к горизонту.
Наложим на систему декартовы координаты, совместив их начало с пушкой и рассмотрим снаряд как материальную точку, участвующую одновременно в двух движениях - по оси х и оси y.
Тогда в некий момент времени t можно записать следующие уравнения для скорости точки:
$\displaystyle v_x=v\cos\alpha \\ v_y=v\sin\alpha-gt$
Уравнение перемещения точки по осям будет иметь вид
$\displaystyle x=vt\cos\alpha \\ y=vt\sin\alpha-\frac{gt^2}{2}$
В любой точке М квадрат расстояния r² от начала координат до этой точки может быть найден по теореме Пифагора. Мы ищем квадрат, чтобы не заморачиваться извлечением квадратного корня, поскольку сама величина r нам не нужна.
$\displaystyle L_M=r_M^2=x_M^2+y_M^2=(vt\cos\alpha)^2+\left(vt\sin\alpha-\frac{gt^2}{2}\right)^2$
Чтобы определить области убывания функции L(t), нужно найти значения t при которых производная L'(t) будет отрицательной.
Упростим L(t), раскрыв скобки и используя основное тригонометрическое тождество, а затем найдем производную.
$\displaystyle L(t)=t^2v^2-vt^3g\sin\alpha+\frac{1}{4}g^2t^4 \\ \frac{dL}{dt}=2tv^2-3vt^2g\sin\alpha+g^2t^3=t(2v^2-3vtg\sin\alpha+g^2t^2)$
Осталось решить неравенство $\displaystyle 2v^2-3vtg\sin\alpha+g^2t^2\ \textless \ 0$
Сначала определим точки, где левая часть обращается в ноль, а потом найдем необходимые интервалы. Получается квадратное уравнение относительно t; его решение тривиально и приводить я его не буду.
Получаем два корня,которые можно записать одним выражением:
$\displaystyle \frac{v}{2g}\left(3\sin\alpha\pm\sqrt{1-9\cos^2 \alpha}\right)$
Отсюда мы получаем область допустимых значений sin(α) ∈ [2√2/3;1] - значение 1 берем из условия, что углы больше 90° не рассматриваются.
С некоторым приближением можно записать α ∈ [70.53°;90°]
Первый (меньший) корень задает нам точку, начиная с которой расстояние между пушкой и снарядом начинает сокращаться.
$t_1=\displaystyle \frac{v}{2g}\left(3\sin\alpha-\sqrt{1-9\cos^2 \alpha}\right)$
Второй (больший) корень задает точку, после прохождения которой расстояние снова начинает увеличиваться.
$t_2=\displaystyle \frac{v}{2g}\left(3\sin\alpha+\sqrt{1-9\cos^2 \alpha}\right)$
Но для t₂ необходимо учесть, что наши формулы рассматривают процесс движения тела до бесконечности, а в реальности снаряд может падать ниже уровня пушки лишь разве что в овраг... Поэтому достаточно ограничиться временем движения снаряда при достижении им горизонта пушки, т.е. у=0 в нашей системе координат.
Для этого находим решение уравнения у=0
$\displaystyle vt\sin\alpha-\frac{gt^2}{2}=0 \\ t\left(v\sin\alpha-\frac{gt}{2}\right)=0 \to t_1=0 \\ v\sin\alpha-\frac{gt_2}{2}=0 \to t_2= \frac{2v\sin\alpha}{g}$
Тривиальное решение t₁=0 нас не интересует, а вот t₂ - то, что нужно.
Окончательно получаем решение
$\displaystyle t \in \left[t_1;\min\left(t_2,\frac{2v\sin\alpha}{g}\right)\right], \\ t_1=\frac{v}{2g}\left(3\sin\alpha-\sqrt{1-9\cos^2 \alpha}\right) \\ \\ t_2=\frac{v}{2g}\left(3\sin\alpha+\sqrt{1-9\cos^2 \alpha}\right) \\ \\ \alpha \in [70.53^\circ;90^\circ]$
Если интересует длительность промежутка времени, в который приближение происходит, она равна
$\displaystyle \min\left(t_2,\frac{2v\sin\alpha}{g}\right)\right]-t_1$
Если минимум равен t₂, получаем решение
$\displaystyle \frac{v}{2g}\left(3\sin\alpha+\sqrt{1-9\cos^2 \alpha}\right)- \frac{v}{2g}\left(3\sin\alpha-\sqrt{1-9\cos^2 \alpha}\right)= \\ \\ \frac{v}{g}\cdot\sqrt{1-9\cos^2 \alpha}, \ \alpha \in [70.53^\circ;90^\circ]$

Эникей_zn (150k баллов) 29 Апр, 18