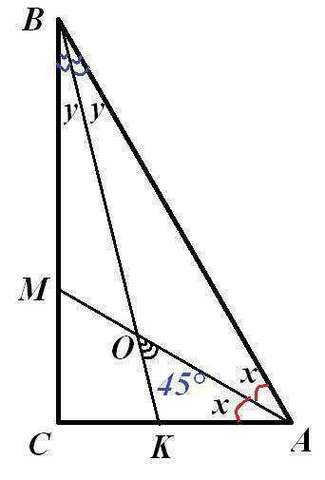
Чертеж - во вложении.
Пусть в Δ АВС биссектрисы ВК и АМ пересекаются точке О, ∠АОК = 45°.
Биссектрисы делят углы треугольника пополам.
Пусть х=∠САМ=∠ВАМ, у=∠АВК=∠СВК.
∠АОВ=180°-45°=135°.
В Δ АОВ по теореме по сумме углов треугольника
х+у+135°=180° ⇒ х+у=45°
В Δ АВС ∠А+∠В+∠С = 180° ⇒ 2х+2у+∠С=180°
⇒ ∠С=180°-2(х+у)=180°-2·45°=90°
Значит, ΔАВС - прямоугольный.