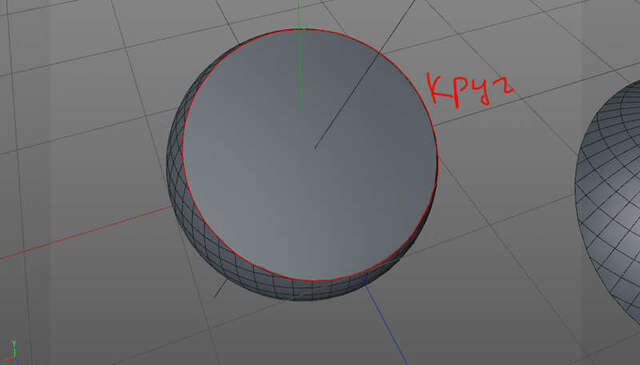
Сечение шара(сферы) плоскостью - всегда является кругом. Центр этого круга - это основание
перпендикуляра(CH), опущенного из центра(C) шара на секущую плоскость. Площадь
круга равна pi*R^2.
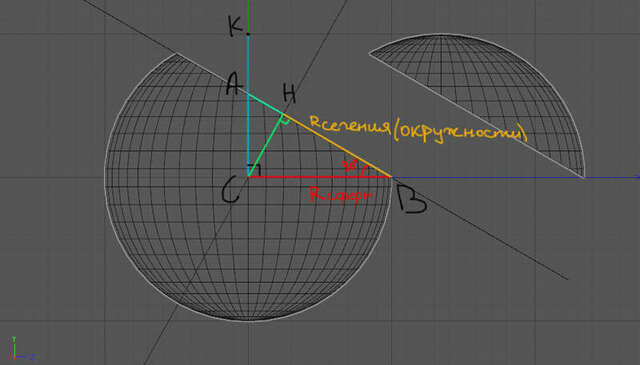
Так как плоскость пересекает шар через конец радиуса, то получаем прямоугольный
треугольник ABC. BC - радиус сферы(собсна, через конец которого и проходит
секущая плоскость), но и KC - тоже радиус сферы(который перпендикулярен радиусу
ВС), а отрезок AC - это часть радиуса КС, которую отсекла секущая
плоскость, CH – высота, опущенная на
гипотенузу АВ. Теперь все сводится к тому, чтобы найти радиус BH
круга(сечения). По условию нам дано, что радиус сферы равен 12, и угол, под
которым плоскость сечет шар - 30°. Рассмотрим прямоугольный треугольник ВНС. ВС - гипотенуза треугольника ВНС, угол НВС
равен 30°. Вспомним, что катет
прямоугольного треугольника, лежащий напротив угла 30° равен половине гипотенузы, следует, что катет НС равен
половине ВС => HC=6. По теореме Пифагора ищем ВН. ВН^2=BC^2-HC^2.
BH^2=144-36. BH=√108.
Все,
теперь ищем площадь сечения(круга). S=pi*R^2 S=pi*(√108)^2
S=108pi.
Ответ:
108pi
(К
слову, пользовался программами Cinema 4D и Photoshop, чтобы показать сечение и треугольник) )0))