Vпирамиды = 1/3 Sh,
где h - высота пирамиды,S - площадь основания
Sосн=1/2аb=6*8:2=24(cм²)
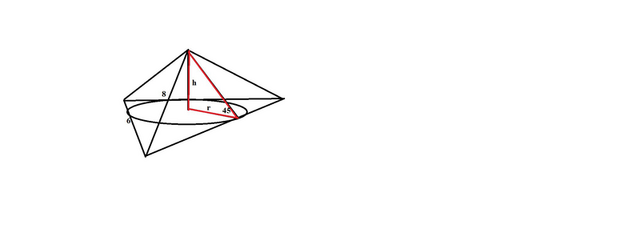
Если все боковые грани наклонены к основанию под одним углом, то основанием высоты пирамиды служит центр вписанной в основание пирамиды окружности.
Радиус вписанной в треугольник окружности находим по формуле:
S=pr (Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.)⇒
r=S/p ,где
р - полупериметр,
r - радиус окружности, вписанной в треугольник.
p=(a+b+c)/2
c=√(a²+b²)=√(6²+8²)=10
p=(6+8+10)/2=12
Sосн=24см²
r=24/12=2
Высоту пирамиды найдем из треугольника, образованного радиусом вписанной окружности, высотой пирамиды и апофемой.В нём угол между апофемой и радиусом равен 45°, а другой - 90°, значит, треугольник равнобедренный.
Тогда высота пирамиды равна радиусу: h=r=2.
V=1/3Sh
V=24*2:3=16(см³)
,