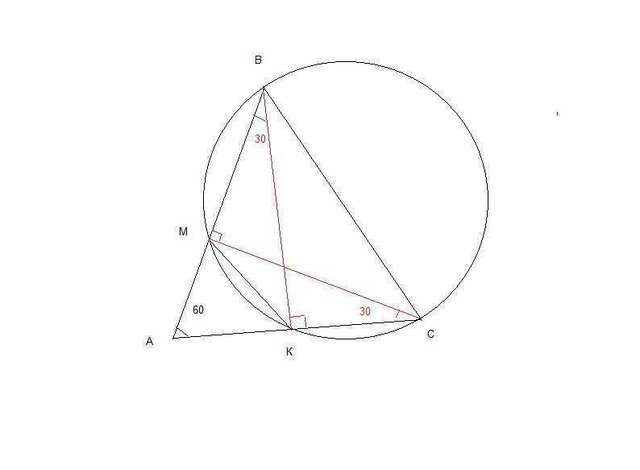
Смотри рисунок.
проведем ВК и СМ . Это будут высота, т.к. треугольники ВСК и ВМС вписаны в окр, ВС- диаметр, значит угол К и М прямой. а углы АВК и АСМ =30
дальше - дело техники
1) треуг. АВС S=АС*ВК/2
из прямоуг. треуг. АМС АС=АМ/sin30=2AM
из треуг. АВК ВК=АК*sin60/sin30=AK√3
подставляем в 1)
S=2AM*AK√3/2
S=AM*AK*√3=7
отсюда АМ*АК=7/√3
но искомое s=(AM*AK/2)*sin60
s=7/(2√3)*√3/2=7/4