Диагональ осевого сечения цилиндра 5 см и образует с основанием угол 30 градусов. Найти...

0 голосов
167 просмотров

Диагональ осевого сечения цилиндра 5 см и образует с основанием угол 30 градусов. Найти объем и площадь полной поверхности.

Геометрия (17 баллов) | 167 просмотров
Дано ответов: 2
0 голосов
Правильный ответ

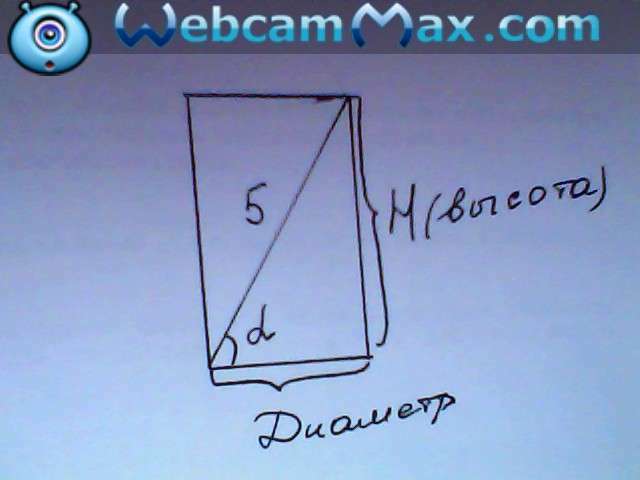
Так как осевое сечение представляет из себя прямоугольник, а диагональ делит его на два прямоугольных треугольника, рассмотрим нижний треугольник:

Так как диагональ, обозначим как D, образует 30 градусов с основанием, тогда имеем высоту цилиндра H равную 2,5.

Диаметр же найдем из прямоугольного треугольника:

 D=\sqrt{D^2-H^2}=\sqrt{5^2-2,5^2}=\sqrt{18,75}

Радиус же будет равен половине диаметра:

R=D/2=\sqrt{18,75}/2

Объем цилиндра равен:

V=SH , где S-площадь основания H-высота цилиндра

Тогда:

V=SH=\pi R^2H

 Получаем:

 V=SH=\pi R^2H=\pi *18,75*2,5=46,875\pi

 Площадь полной поверхности равна:

Sполной=2Sоснования+Sбоковой поверхности

Имеем:

 S=2\pi R^2 + 2\pi RH

S=\frac{2*18,75\pi}{4}+\frac{2*2,5*\sqrt{18,75}\pi}{2}=\frac{18,75\pi}{2}+2,5\sqrt{18,75}\pi

 

Рисунок рассматриваемого треугольника во вложении

 

image
(9.1k баллов)
0 голосов

АА1В1В — прямоугольник

Из ΔАВ1В:

AB=2R=5*sin30град.=5/2=2.5 см.

R=1.25 см.

H=B(1)B=5*cos30град.=5 под корнем3/2=2,5 под корнем 3 см.

S(осн.)=ПR^2=П(1.25)^2=П*1.56=1.56П см^2.

я нашла высоту, радиус и площадь основания цилиндра.

 
Похожие задачи