Решите,пожалуйста,неравенство: 3х^2-12 деленное ** 1-11х>0

Question

Решите,пожалуйста,неравенство: 3х^2-12 деленное на 1-11х>0

Answer 1

0" alt="\frac{3x^2-12}{1-11x}>0" align="absmiddle" class="latex-formula">

Нули числителя:

 

 

 

 

 

Нули знаменателя:

 

Прямая:///+///(-2)...-...(1/11)///+///(2)...-... 

 

Ответ: 

 

 

 

 

 

 

 

 

Answer 2

0\\f(x)=\frac{3x^2-12}{1-11x}\\D(f):1-11x\neq0\\.\ \ \ \ \ \ \ \ x\neq\frac{1}{11}\\f(x)=0\\\frac{3x^2-12}{1-11x}=0\\3x^2-12=0\\x^2=4\\x=2\ \ \ \ \ x=-2" alt="\frac{3x^2-12}{1-11x}>0\\f(x)=\frac{3x^2-12}{1-11x}\\D(f):1-11x\neq0\\.\ \ \ \ \ \ \ \ x\neq\frac{1}{11}\\f(x)=0\\\frac{3x^2-12}{1-11x}=0\\3x^2-12=0\\x^2=4\\x=2\ \ \ \ \ x=-2" align="absmiddle" class="latex-formula">

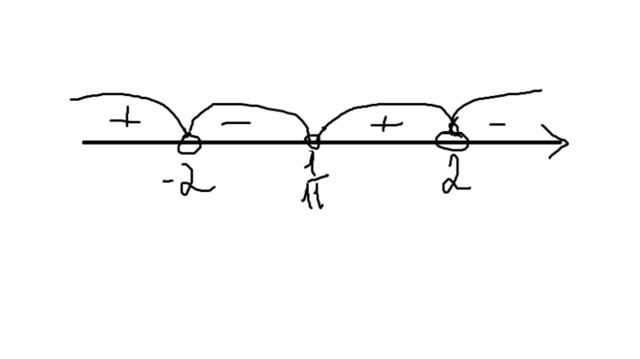
Наноси на координатную прямую 2;-2;1/11. Опредделяем знаки на интервалах.

---