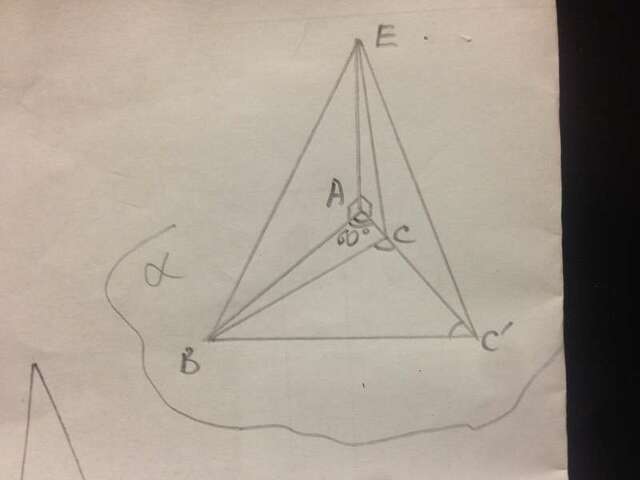
ЕВ и ЕС - наклонные к плоскости α, ЕА - перпендикуляр к плоскости α, ЕВ=4√5 см, АВ=8 см, ∠ВАС=60°, ВС=7 см.
ЕА=√(ЕВ²-АВ²)=√(80-64)=4 см.
В тр-ке АВС АС=х. По теореме косинусов ВС²=АВ²+ВС²-2АВ·ВС·cos60,
49=64+х²-2·8·х/2,
х²-8х+15=0,
х₁=3, х₂=5.
АС=3 см, АС`=5 cм.
Задача имеет два решение. Такое возможно, ведь в тр-ка ВАС и ВАС` BC=BC`=7 см и тр-ник ВСС` - равнобедренный.
1) В тр-ке ЕАС ЕС=√(ЕА²+АС²)=√(16+9)=5 см.
2) В тр-ке ЕАС` ЕС`=√(EA²+AC`²)=√(16+25)=√41 см.
Ответ: вторая наклонная равна 1) 5см, 2) √41 см.