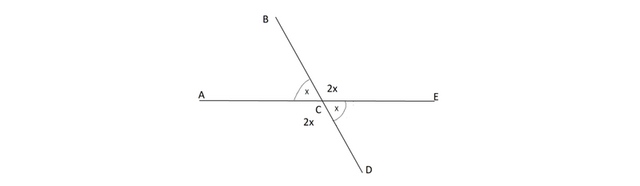
Сделаем простой рисунок и рассмотрим его.
Сумма углов, получающихся при пересечении двух прямых, равна 360 градусов.
Для угла АСВ смежными являются углы ВСЕ и АСD
Из условия задачи известно, что
∠ВСЕ+∠ACD=4∠АСВ
Cумма смежных с углом АСВ углов равна
∠ВСЕ+∠ACD=360° -∠АСВ-∠DCE
Но ∠АСВ=∠DCE как вертикальные углы.
Поэтому
∠ВСЕ+∠ACD=360-2∠АСВ
360° - 2∠АСВ=4∠АСВ
6∠АСВ=360°
∠АСВ=360°:6=60°
Сумма смежных с углом АСВ углов равна 60*4=240°
Проверим:
∠ВСЕ+∠ACD+АСВ+DCE=
240°+60°+60°=360°
----------
По какой-то причине знак угла в некоторых местах иногда выглядит прямоугольником. На результат решения это не влияет.