Пусть g(x)=x/(x+1)
Функция f определена на интервале [0;1).
Найдем, при каких х дробь x/(x+1) принадлежит указанному интервалу.
Решаем неравенство:
0≤х/(х+1) < 1,
которое равносильно системе неравенств:
{x/(x+1) >0;
{x/(x+1)-1<0.<br>
или
{x/(x+1) >0;
{-1/(x+1)<0.<br>
{x+1>0
{x≥0
Решением данного неравенства является х≥0 или х∈[0;+∞)
2 способ.
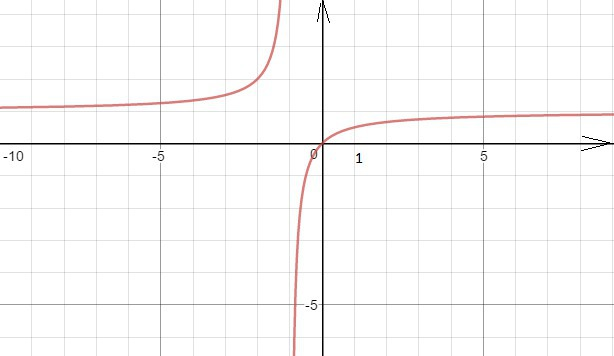
Построим график функции g(x)=x/(x+1).
Выделим целую часть
g(x)=(x+1-1)/(x+1);
g(x)=1-(1/(x+1))- гипербола
Cм. рисунок в приложении
Найдем при каких х
g(x)∈[0;1)
0≤g(x)<1 ⇒ 0≤x< + ∞ <br>или
х∈[0;+∞)
О т в е т. D(f(x/(x+1))=[0;∞)