В остроугольном треугольнике ABC высоты AA1 и BB1 пересекаются в точке О и величина угла...

Question

В остроугольном треугольнике ABC высоты AA1 и BB1 пересекаются в точке О и величина угла AOB=6. Найти площадь треугольника ABO, если АА1= 3 см и ВВ1 = 5 см.
( я тут не много набросал, помогите кто знает как решить)

---

Comments

Что значит величина угла AOB равна 6? Евляется ли треуг. Равнобедренным?

---

Угол AOB 60 градусов

---

Если он равнобедренный не сказано, сказано что он устоугольный

---

На рисунке AOB1 60.определись, парень

---

AOB не может быть 60 градусов, поскольку угол AB1O равен 90 градусов, то есть в треугольнике AOB1 углы OAB1 и AOB1 острые. Угол AOB1 является смежным к углу AOB. Следовательно, угол AOB тупой и не может быть равен 60 градусов....Возможно, тут AOB1 = 60 градусов все-таки...

---

Да, верно, так решения никто не знает?

Answer 1

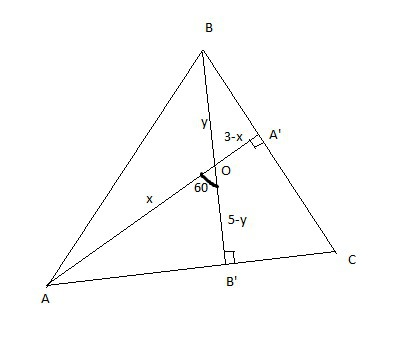
Обозначим AO=x, OA1=3-x, BO=y, OB1=5-y.
Тогда из треугольника AOB1: OB1=AO*cos∠AOB1,
Из треугольника A1OB: A1O=BO*cos∠BOA1
Получим систему уравнений
5-y=x*cos(60°)
3-x=y*cos(60°)
_____
2(5-y)=x
2(3-x)=y
______
10-2y=x
6-2x=y
_____
Подставим первое уравнение во второе. Получим:
6-2(10-2y)=y
6-20+4y=y
y=14/3
x=10-2*(14/3)=2/3
Тогда S_AOB=1/2*AO*OB*sin∠AOB=1/2*x*y*sin(120°)=1/2*2/3*14/3*√3/2=7√3/9

---