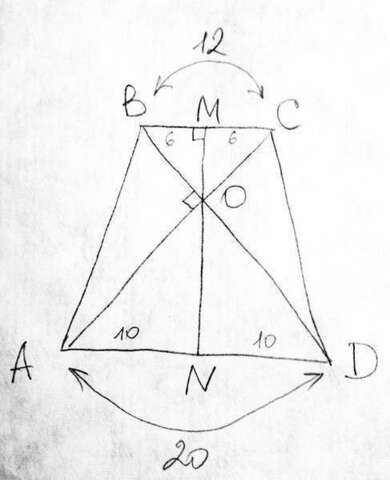
Треугольники ВОС и АОД - прямоугольные и равнобедренные, т. к. трапеция равнобедренная.
Высота проходящая через точку пересечения диагоналей будет осью симметрии. И делит указанные выше треугольники точно пополам
Получившиеся треугольники ОМС и ОМВ - тоже равнобедренные, тк у них один угол = половина ПРЯМОГО УГЛА (пересечение перпендикулярных диагоналей) , а второй угол =90 градусов (т. к. высота) . Поэтому на третий тоже остаётся половина 90 градусов. Т. е. углы при основаниях равны, след-но треугольник равнобедрен.
А это значит, что ВМ=МО. Но ВМ = половинка ВС, которая =12, т. е. ВМ=6=МО=6. Так?
Аналогично рассматривает треугольник АОД, который тоже равнобедрен, который тоже высота делит пополам на два равнобедренных, а значит NO=ND=NA=10
А высота всей трапеции = NO+OM=6+10 = 16.
А площадь = (ВС+АД) *MN/2