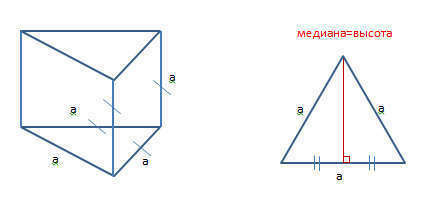
Все очень просто: дана замечательная призма, у которой все грани равны (смотри прикрепленный файл). Если мы найдем сторону основания - мы сможем вычислить всё, что угодно, тк сторона основания равна всем остальным рёбрам.
1) обозначим все грани (пусть это будет а)
2) если призма правильная, то в ее основании лежит равносторонний треугольник; следовательно медиана этого треугольника - это его высота. Мало того, медиана делит основание пополам, (то есть мы можем работать с прямоугольным треугольником).
3) по т. Пифагора: a^2=2^2+(1/2a)^2;
4) Сделав нехитрые вычисления, получаем: a^2=16/3
5) Ищем Sбок=3*a^2 (тк каждая боковая грань - есть квадрат со стороной а, как дано в условии). Получаем: Sбок=3*16/3=16.
Ответ: 16