Построим график уравнения у = |-x²-х+1|
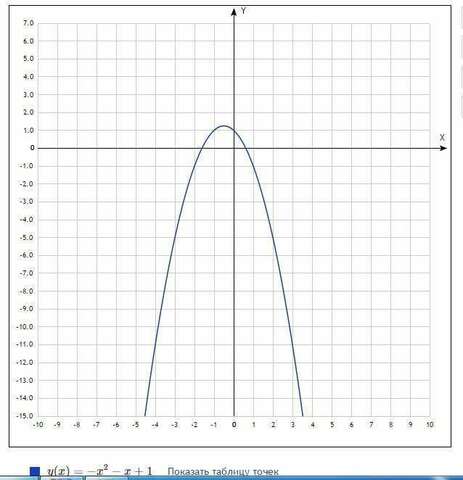
Для этого сначала строим график уравнения у = -x²-х+1.
Видно что графиком будет парабола, направленная ветвями вниз. Найдём её вершину:
x0 = -b/2a = 1/(-2) = -0.5
y0 = f(x0) = - (-0.5)² + 0.5 + 1 = 1.25
Значит вершина параболы находится в точке (-0.5; 1.25).
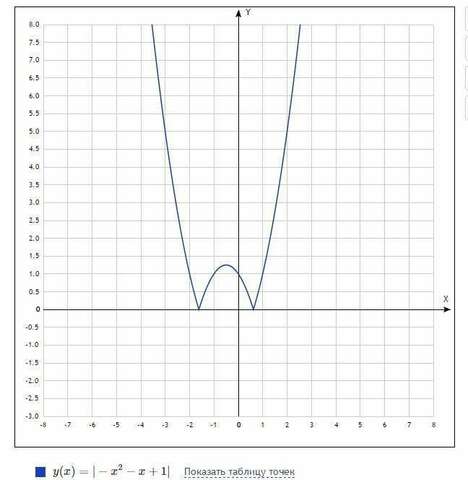
Построив параболу (картинка 1), строим график уравнения у = |-x²-х+1|. Всё что находится на нашем графике ниже оси Оу отображаем симметрично этой же оси. Всё что выше - оставляем без изменений. У вас должен получиться график, показанный на картинке 2.
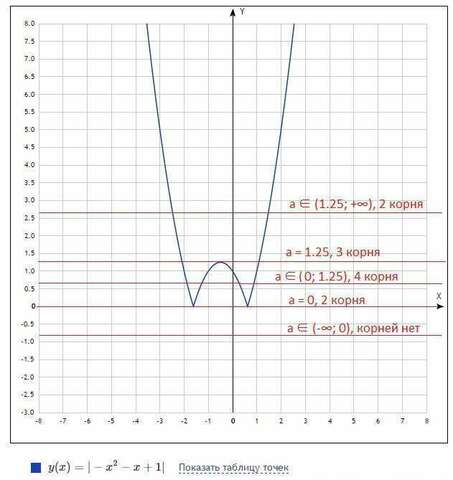
а - семейство прямых, параллельных оси Oy. Эти прямые разбивают всю плоскость на различные интервалы. В каждом из интервалов существует определенное количество корней, в зависимости от значения параметра а (см. картинку 3). Конкретно, для а ∈ (-∞; 0), корней нет (т.к. весь график лежит выше или на оси Оу). Для а = 0, имеем 2 корня, для а ∈ (0; 1.25) - 4 корня, для а = 1.25 - 3 корня, для а ∈ (1.25; +∞), 2 корня.
Легко заметить, что уравнение имеет ровно 3 корня только при одном значении параметра, при а = 1.25.
Ответ: при а = 1.25 .