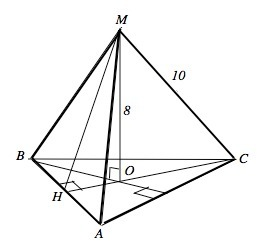
Основанием данной пирамиды является правильный треугольник, а вершина пирамиды проецируется в его центр ( общую точку пересечения высот, биссектрис, медиан).
Обозначим пирамиду МАВС.
Высота МО=8 см, ребра равны 10 см.
Проведем СН⊥АВ⇒ ВН=АН
Из ∆ ВОМ катет ВО=6 см ( египетский треугольник)
В ∆ ВОН угол ОВН=30°, ⇒ ВН=ВО•cos30°=3√3.
АВ=2•ВН=6√3
Из ∆ ВМН апофема МН=√(BM²-BH²)=√(100-27)=√73
Ѕ(бок)=3•Ѕ(АВМ)=3•МН•АВ÷2=3•(√73)•3√3=133,1878
Ѕ(АВС)=0,5•AB²•sin60°=18•3•√3:2=27√3=46,7654
Ѕ (полн)=9•√219)+27√3=179,953 см²