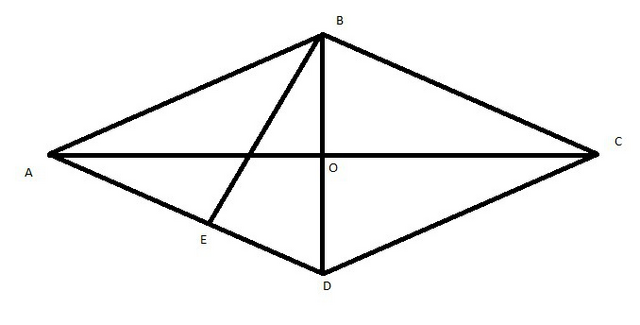
Сторона ромба равна 20/4=5.
Высота ромба BE равна 2.5.
Из треугольника ABE: sin∠A=2.5/5=1/2.
cos∠A=√(1-sin²∠A)=√3/2
Отсюда из треугольника ABD найдем первую диагональ BD по т. косинусов:
BD²=AB²+AD²-2*AB*AD*cos∠A=5²+5²-2*5*5*√3/2=50-25√3
BD=√(50-25√3)=5√(2-√3)=5(√6-√2)/2
Так как ∠A+∠B=180°, то cos∠B=-cos∠A=-√3/2.
Тогда из треугольника ABC по т. косинусов найдем вторую диагональ AC:
AC²=AB²+BC²-2AB*BC*cos∠B=5²+5²+2*5*5*√3/2=50+25√3
AC=√(50+25√3)=5√(2+√3)=5(√6+√2)/2