1. Указать наибольшее целое решение неравенства х 2

$x^2-8x+12\ \textless \ 0$

Квадратные неравенства решаются путём их представления в виде уравнения, нахождения корней и значений икс, принадлежащих промежутку, обусловленному знаком и коэффициентом, стоящим после него. Так, $x^2-8x+12=0$ – квадратное уравнение, полученное из квадратного неравенства. Решаем его, чтобы найти корни.

$x^2-8x+12=0\\D=\sqrt{(-8)^2-4*1*12}=\sqrt{64-48}=\sqrt{16}=4\\x_1=\frac{8+4}{2}=6\\x_2=\frac{8-4}{2}=2$

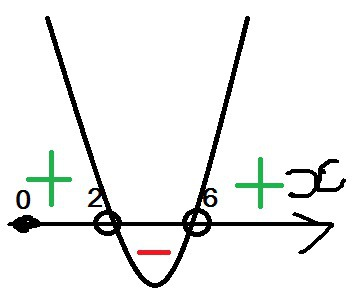
Теперь чертим ось X, отмечаем на ней данные корни и смотрим, при каких значениях икс функция меньше нуля. (График в приложении)
Так как $x^2$ , то и ветви параболы направлены вверх. Точки не закрашены, так как неравенство строгое.

Ответ: x∈(2; 6)

1. Указать наибольшее целое решение неравенства х 2 – 8х + 12 < 0