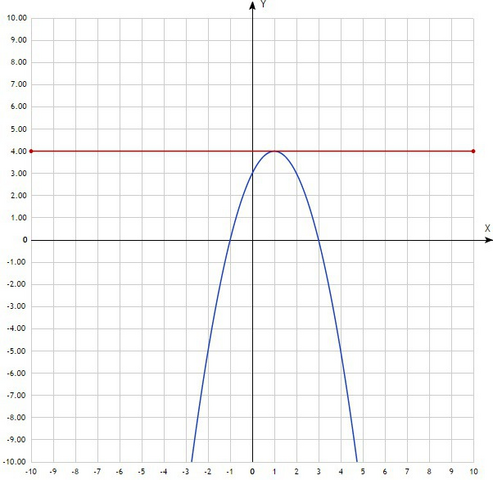
Угловой коэффициент в точке касания есть производная функции в этой точке. Найдём производную функции f(x)=3+2x-x²:
f'(x)=(3+2x-x²)=2-2x
Теперь значение производной функции в точке х₀:
f'(x₀)=2-2*1=0
Угловой коэффициент касательной в точке касания равен k=0, то есть касательная параллельна оси абсцисс.
Уравнение касательной:
y=f(x₀)+f'(x₀)(x-x₀)
f(x₀)=3+2*1-1=4
y=4+0*(x-1)=4 - прямая, параллельная оси абсцисс, проходящая через точку y=4.