Образующая конуса равна b и наклонена к основанию под углом a. Найти 1) радиус вписанного...

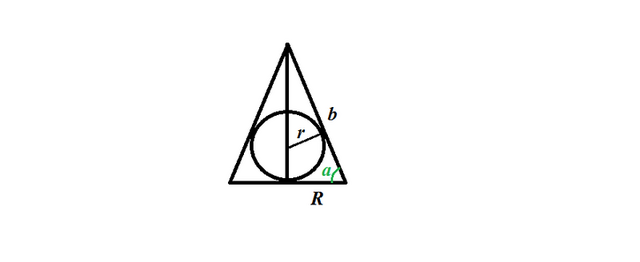
Радиус окружности вписанной в треугольник вычисляется по формуле:

$r=\frac{S}{P}$ где S-площадь треугольника а P-его периметр.

Исходя из геометрии задачи и приложенного рисунка, найдем радиус конуса:

$cos\alpha=\frac{R}{b}$

Откуда $R=bcos\alpha$

Найдем высоту конуса:

$h=bsin\alpha$

Тогда площадь треугольника равна:

$S=h*R=\frac{b^2sin2\alpha}{2}$

Найдем его периметр:

$P=2h+R=2b(sin\alpha+cos\alpha)$

Тогда радиус вписанной окружности равен:

$r=\frac{S}{P}=\frac{\frac{b^2sin2\alpha}{2}}{2b(sin\alpha+cos\alpha)}$

Тогда объем этой сферы будет равен:

$V=\frac43\pi r^3=\frac43\pi (\frac{\frac{b^2sin2\alpha}{2}}{2b(sin\alpha+cos\alpha)})^3$