С₁) для решения этого уравнения нужно знать две формулы


(см. фото 1)
С₂) (см.фото 2)
На верхнем рисунке О₁О₂=О₁С+О₂С=11+21=32
Перечертим трапецию О₁АВО₂
∠АО₁О₂=60°
Проведем высоту О₁Н. ∠НО₁А=∠О₁НО₂=90°
∠НО₁О₂=90°-60°=30°
Рассмотрим прямоугольный Δ О₁НО₂:
НО₂=О₁О₂*sin30°=32*0.5=16
O₁H=О₁О₂*cos30°=32*√3/2=16√3
Проведем вторую высоту АН₁=О₁Н=16√3
О₁АН₁Н-прямоугольник, значит O₁A=НН₁=11
Н₁О₂=НО₂-НН₁=16-11=5
Н₁В=Н₁О₂+О₂В=5+21=26
теперь из прямоугольного ΔАН₁В находим АВ
АВ²=АН₁²+Н₁В²=(16√3)²+26²=1444
АВ=√1444=38
ОТВЕТ: 38
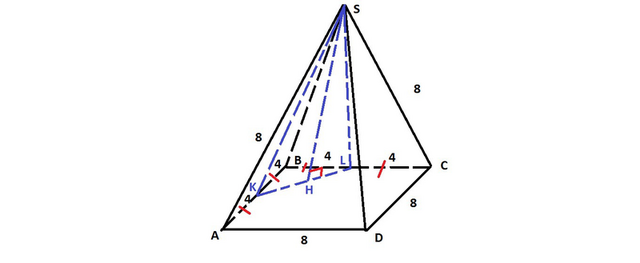
С₃) см. рисунок
Пусть точка К - середина АВ, точка L-середина ВС
построение сечения:
К и L лежат в одной плоскости АВС, значит соединяем эти точки.
S и К лежат в одной плоскости SAB, значит соединяем эти точки.
S и L лежат в одной плоскости SBC, значит соединяем эти точки.
Итак, сечением является ΔSKL.
Четырехугольная пирамида правильная, значит в основании квадрат.
АК=АВ/2=8/2=4
АК=ВL=4
KL=√(АК²+ВL²)=√(4²+4²)=4√2
SK и SL - являются медианами и высотами равнобедренных треугольников АSB и SBC- соответственно.
Для прямоугольных треугольников KBS и LBS BS-общая гипотенуза, КВ=ВL, следовательно ΔKBS=ΔLBS - по катету и гипотенузе, значит SK=SL
SL=SK=√(SB²-AK²)=√(8²-4²)=√48=4√3
В равнобедренном ΔSKL проведем высоту SH ( она же и медиана), следовательно HL=KL/2=4√2/2=2√2
SH=√(SL²-HL²)=√( (4√3)²- (2√2)² )=√40=2√10
S=KL*SH/2=4√2 * 2√10 / 2=8√20/2=4√(4*5)=8√5
ОТВЕТ: 8√5
С₄) (4х-х²)²-32√(4х-х²)=а²-14а
рассмотрим отдельно функции
у=(4х-х²)²-32√(4х-х²) и у=а²-14а
для функции у=(4х-х²)²-32√(4х-х²) найдем область значения
(смотри последние 2 фото)
Итак получаем, что функция у=(4х-х²)²-32√(4х-х²) изменяется от -48 до 0.
функция у=а²-14а - не содержит аргумента, то есть х. Значит эта функция вида у=с (горизонтальная прямая)
значит у=а²-14а тоже должна изменятся от -48 до 0, чтобы было пересечение с графиком функции у=(4х-х²)²-32√(4х-х²)

a∈[0;6] U [8;14]
Ответ: a∈[0;6] U [8;14]