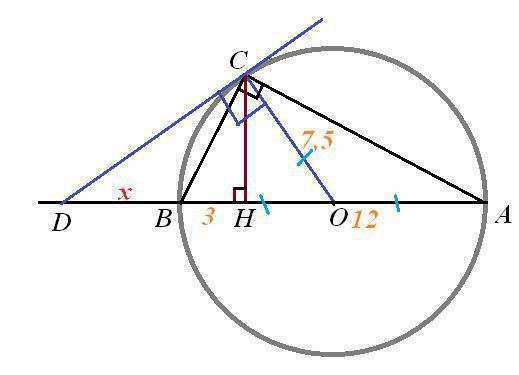
Пусть О-центр окружности.
По свойству касательной r=OC⊥CD ⇒ Δ OCD - прямоугольный, ∠С=90°.
По свойству высоты прямоугольного треугольника, опущенной на гипотенузу, СН² = ВН·НА ⇒ СН² = 3·12=36 ⇒ СН=6.
АВ - диаметр, АВ=3+12=15 ⇒ r=OA=OB=OC=7,5.
Пусть BD=x.
По свойству касательной и секущей к окружности, проведенных их одной точки, CD² = DB·DA = x·(x+15).
C другой стороны в прямоугольном Δ CDН по теореме Пифагора
CD²=НD²+НC² = (x+3)²+6².
Решаем уравнение (x+3)²+6² = x·(x+15)
х²+6х+9+36 = х²+15х
9х = 45
х = 5
Значит, BD = 5.
Ответ: 5.