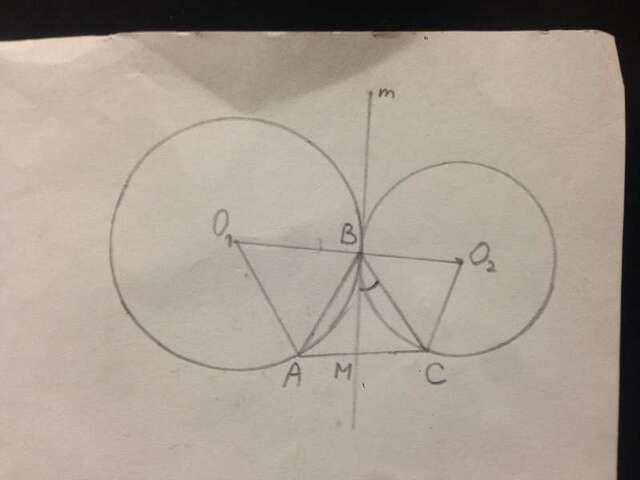Две окружности с радиусами R и к (R>r) касаются в точке А. Определите длину стороны...

R=О1В=5, r=О2В=3. АВС - равносторонний треугольник. m - общая касательная.
Пусть ∠МВС=х, тогда ∠АВМ=60-х.
Углы МВС и АВМ - углы между касательной и хордой, значит ∠АО1В=2(60-х) и ∠СО2В=2х.
Формула хорды: l=2Rsin(α/2), где α - градусная мера хорды.
АВ=2·О1В·sin(60-х)=2R·sin(60-x),
ВС=2·О2В·sinx=2r·sinx,
АВ=ВС, значит
2R·sin(60-x)=2r·sinx,
2·5(sin60·cosx-cos60·sinx)=2·3sinx,
10(√3cosx/2-sinx/2)=6sinx,
5√3cosx-5sinx=6sinx,
11sinx=5√3cosx,
11tgx·cosx=5√3cosx,
tgx=5√3/11.
-----------------------------------------------
tg²x+1=1/cos²x,
tg²x+1=1/(1-sin²x),
1-sin²x=1/(tg²x+1),
sin²x=1-[1/tg²x+1)],
$sin^{2}x=1- \frac{1}{tg^{2}x+1 } =1- \frac{1}{ \frac{75}{121}+1 } =1- \frac{121}{196} = \frac{75}{196}$
sinx=5√3/14.
------------------------------------------------
Итак, ВС=2r·sinx=6·5√3/14=15√3/7≈3.7 см - это ответ.