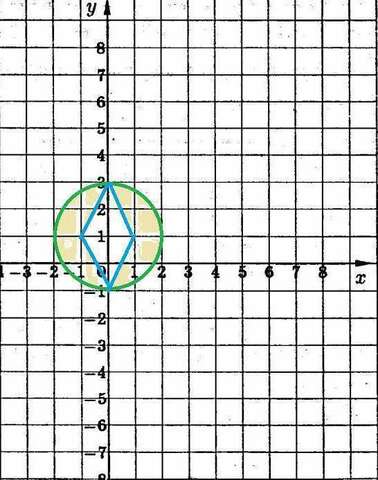
S=S(круга)-S(ромба)=πR²-(1/2)·d₁·d₂=π·2²-(1/2)·4·2=4π-4 кв. ед.
х²+y²-2y≤3 ⇒ x²+(y-1)²≤4- внутренняя часть круга радиуса R=2 с центром в точке (0;1).
2|x|+|y-1|≥1
Раскрываем модуль:
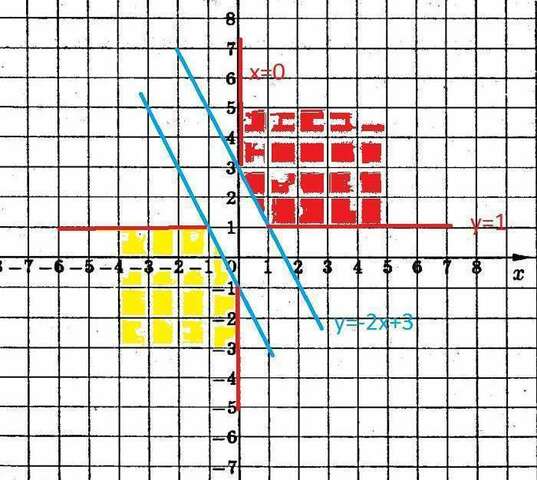
1) х≥0; у-1 ≥0 получаем 2х+у-1≥2 или у≥-2х+3 часть плоскости ограниченная тремя неравенствами х≥0; у≥1; у≥-2х+3 ( см. рис. 2) красного цвета
2) х<0; y-1<0 получаем неравенство -2x-y+1≥2 или у ≤-2х-1<br> Часть плоскости, ограниченная тремя неравенствами х<0; у<1; у≤-2х-1 ( см. рис. 2) желтого цвета<br>и аналогично
3) x≥0; y-1<0 получаем неравенство 2х-у+1≥2 или у≤2х-1<br>Часть плоскости, ограниченная неравенствами х≥0; у< 1; y ≤2х-1
4) x<0; y-1≥0 получаем неравенство -2х+у-1≥2 или у≥2х+3.<hr>