Основанием прямого паралелипипита является паралелограм,стороны 3 и 4 см,образуют угол 60...

Question

Дан 1 ответ

Правильный ответ

Объем находится по формуле

$V=S_{Osnovanija}*H$

$S_{Osnovanija}$ -- это площадь основания параллелепипеда, которая в данном случае является параллелограммом.

H - высота параллелепипеда.

Самое нетрудное, это найти площадь параллелограмма в основании по формуле

$S=a*b*\sin 60^\circ$

Значит

$S_{Osnovanija}=3*4*\sin 60^\circ$

$S_{Osnovanija}=3*4*\frac{\sqrt{3}}{2}$

$S_{Osnovanija}=6\sqrt{3}$

Поэтому

$V=6\sqrt{3}*H$

Найти H сложнее.

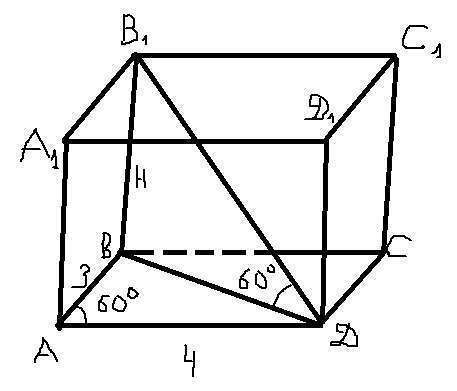
Рассмотрим рисунок. BD - меньшая диагональ параллелограмма в основании. Так как лежит напротив угла в 60 градусов со сторонами в 3 см и 4 см. Другая диагональ АС будет лежать напротив угла в 120 градусов c теми же длинами сторон. Напротив большего угла лежит большая сторона. Прямоугольный треугольник ВВ1D состоит из стороны BD и высоты H. Значит B1D - меньшая диагональ параллелепипеда.

Ведь если будем рассматривать диагональ АС1, то она будет длиннее, чем B1D.

Из прямоугольного треугольника ВВ1D найдем высоту, которая равняется ВВ1. Этот треугольник прямоугольный, так как ВВ1 перпендикулярен всей плоскости основания по определению. Найти ВВ1 можно, если найти любую другую сторонц этого треугольника. В данном случае найти диагональ параллелепипеда B1D непонятно как. А вот диагональ в основании параллелепипеда BD можно найти по теореме косинусов.

$BD^2=AB^2+AD^2-2*AB*AD*\cos\angle A$