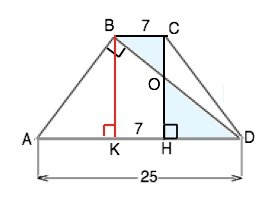
Диагональ равнобедренной трапеции перпендикулярна боковой стороне, а основания равны 7 см и 25 см. Найдите длины отрезков, на которые диагональ делит высоту трапеции, проведенную из тупого угла.
———
Обозначим трапецию АВСD.
ВС=7, АD=25.
Опустим из вершин тупых углов высоты ВК и СН на основание АD.
Высота равнобедренной трапеции, опущенная на большее основание, делит его на отрезки, меньший из которых равен полуразности оснований, а больший - их полусумме.
АК=(АD-ВС):2=(25-7):2=9
КD=(АD+ВС):2=(25+7):2=16
∆ АВD - прямоугольный по условию.
Высота прямоугольного треугольника есть среднее пропорциональное между отрезками, на которые она делит гипотенузу.
ВК²=АК•КD=9•16
ВК=√(9•16)=3•4=12
О - точка пересечения диагонали ВD и высоты СН.
Рассмотрим ∆ ВОС и ∆ BOD
Их углы равны: при О - как вертикальные, остальные - накрестлежащие.
∆ ВОС~∆ BOD по равным углам. Из подобия следует отношение:
ВС:НD=СО:ОН
Примем СО=х
Тогда ОD=12-x, и
7:9=х:(12-х)
84-7х=9х
16х=84 ⇒ х=5,25
СО=5,25 см
ОH=12-5,25=6,75 см