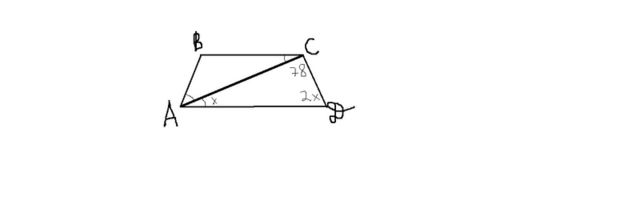
Построив рисунок, получаем:
1). ∠ACD=78°. ∠BAC=∠CAD=x°, т.к. по условию AC - биссектриса. ∠BAC=∠CDA=2x°, т.к. по условию ABCD - равнобедренная трапеция (значит углы при основании AD равны).
2). Рассмотрим треугольник ACD. По свойству сумма всех углов равна 180°, т.е. ∠CAD+∠ACD+∠CDA=180°. Подставив вышеуказанные данные, получаем x°+78°+2x°=180°. 3x°=102°. x=34°.
3). ∠BAD=2x=68°. ∠CDA=∠BAD=68°. ∠BCD=78°+∠BCA. ∠BCA=∠CAD=x°=34°, как накрест лежащие углы при параллельных прямых AD и BC и секущей AC (AD и BC параллельны как основания трапеции ABCD). Тогда ∠BCD=78°+34°=112°.
4). ∠ABC=360°-∠BAD-∠CDA-∠BCD (сумма всех углов трапеции равна 360°). ∠ABC=360°-68°-68°-112°=112°. Итого, все углы трапеции ABCD найдены.