Задание 1

Приравниваем обе части к нулю. Помним, что знаменатель нулю быть равен не может, поэтому решения знаменателя будут выколоты.
Числитель:
х-1=0 х+5=0 х-4=0
х=1 х=-5 х=4
Знаменитель:
х²=0 х²-х+1=0
х=0 D<0, Решений нет.</p>
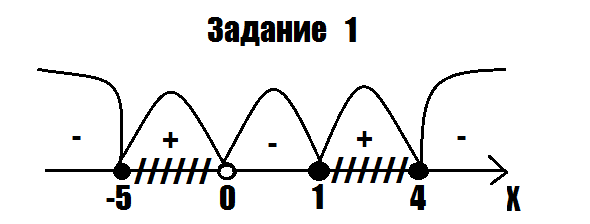
Согласно чертежу ("Задание 1") получаем:
Ответ: [-5;0), [1;4]
Задание 2

Система разных уравнений решается так:
1) Cогласно правилу, в рабочей зоне приравниваем к нулю квадратное уравнение, а дальше решаем квадратное неравенство (1-ое неравенство)
x²-2x-3=0
x₁+x₂=2
x₁*x₂=-3
x₁=3, x₂=-1
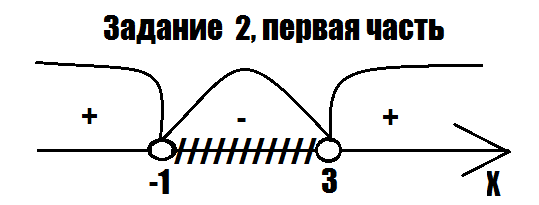
Согласно чертежу ("Задание 2, первая часть") получаем ответ (-1;3)
2) Решаем второе неравенство.
6-3х≤0
-3х≤-6 | : (-3)
х≥2
3) Пишем в системе ответы, полученные при отдельном решение и изображаем в одном чертеже, на пересечении получаем ответ.
{-1
{x≥2
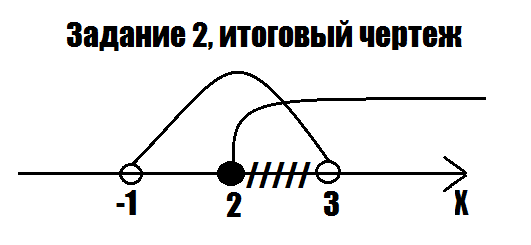
С помощью итогового чертежа ("Задание 2, итоговый чертеж") получаем ответ к системе неравенств: [2;3)
Ответ: [2;3)