Помогите пожалуйста с решением. Заранее СПАСИБО! Вычислите площадь треугольника,...

Question

Помогите пожалуйста с решением. Заранее СПАСИБО!
Вычислите площадь треугольника, ограниченного осями координат и касательной к графику функции y=4 -√(4x+5) в точке с абсциссой х0=1.

Answer 1

Уравнение касательной 
y=y'(1)(x-1)+y(1)

y'=-4/(2√(4x+5))=-2/√(4x+5)
y'(1)=-2/3
y(1)=4-3=1

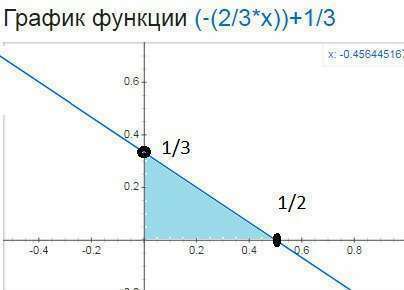
y=-(2/3)(x-1)+1=-(2/3)x-(2/3)+1=-(2/3)x+1/3 
найдем точки пересечения касательной с осями координат
х=0, y=1/3                      (0;1/3)
y=0,  (2/3)x=1/3  x=1/2   (1/2;0)

площадь прямоугольного треугольника 
S=ab/2= (1/2)(1/3)/2=1/12

---