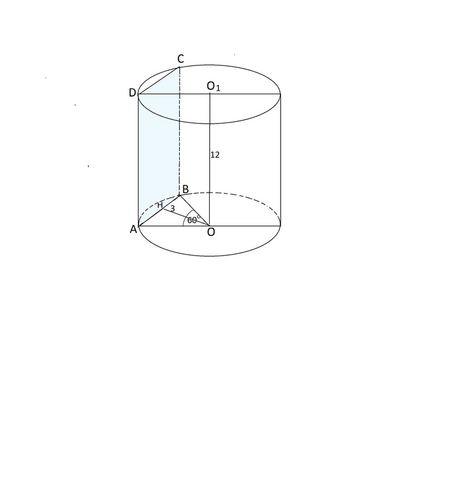
В цилиндре параллельно оси проведена плоскость, отсекающая от окружности основания дугу в 60 градусов. Длина оси 12 см,
ее расстояние от секущей плоскости 3 см.
Вычислить площадь сечения
Площадь сечения - это площадь прямоугольника АВСD.
Высота ВС его равна длине оси цилиндра и равна 12 см.
Сторону АВ нужно найти.
Так как дуга АВ равна 60°, центральный угол АОВ =60°,
отсюда и углы треугольника АОВ при АВ равны 60°, т.к. АО=ВО.
Треугольник АОВ - равносторонний.
АВ=АО=ВО.
ОН- высота этого треугольника, противолежит углу 60°.
АВ=АО=ОН: sin( 60°)
АВ=3: sin( 60°)=3:(√3):2=6: √3=6√3):√3·√3=2√3
S сечения =12·2√3=24√3 см²