Понятно, что a>=0.
Левая часть переписывается как |x|^2 - 8|x| + 12, поэтому если x=b корень уравнения, то и x=-b - корень.
Так как уравнение должно иметь 6 корней, то возможен только такой случай: уравнение имеет ровно 3 положительных корня.
Таким образом, уравнение |x^2-8x+12| = a должно иметь ровно 3 положительных корня. Но это уравнение можно записать как совокупность двух уравнений:
[ x^2-8x+(12-a)=0, x^2-8x+(12+a)=0 ]
Заметим, что по теореме Виета если второе уравнение имеет корни, то все они положительны (т.к. сумма корней 8, а произведение положительно и равно 12+a).
1 случай. Второе уравнение имеет 1 корень, а первое уравнение - 2 положительных корня.
Несложно убедиться, что первое условие выполняется только при a=4. Подставим в первое уравнение а=4:
x^2-8x+8=0
D/4=16-8=8>0
уравнение имеет 2 корня, а из теоремы Виета следует, что эти корни положительны.
Итак, при a=4 уравнение имеет нужное число корней.
2 случай. Второе уравнение имеет 2 корня, а первое имеет корни разных знаков.
Для того, чтобы узнать, когда выполняется первое условие, вычислим дискриминант:
D/4=16-12-a=4-a>0, откуда a<4.</p>
Для того, чтобы выполнялось второе условие, нужно чтобы 1) корни были и 2) ихз произведение было отрицательно.
D/4=16-12+a=4+a>0 - верно для всех а>0
12-a<0, откуда a>12.
Очевидно, такой случай невозможен.
3 случай. Второе уравнение имеет 2 корня, а первое - один корень, который положителен.
Понятно, что у первого уравнения 1 корень будет только при a=-4, но a>0. Противоречие.
Итак, уравнение имеет 6 корней только при a=4, это число и идет в ответ.
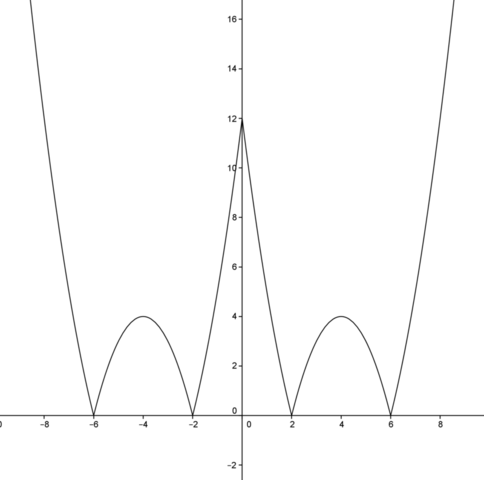
P.S. Традиционный способ решения таких задач - графический. Для того, чтобы понять, сколько корней имеет уравнение f(x)=a, нужно всего лишь построить график y=f(x), а затем смотреть, при каких a прмая y=a пересекает график в нужном количестве точек. График |x^2-8|x|+12|=y см. во вложении. Как правило, такой способ приводит к ответу быстрее, чем аналитическое решение.