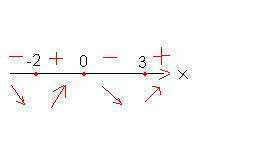Находим производную данной функции.
f'(x)=4*3/4x^3-3x^2-18x+0
f'(x)=3x^3-3x^2-18x
3x^3-3x^2-18x=0
x^3-x^2-6x=0
x(x^2-x-6)=0
Из т.Виета:
х1=3
х2=-2
х(х+2)(х-3)=0
Значения, обращающие в нуль: 0, -2, 3
То есть возрастает на [2; 0] и [3; +inf)
Убывает на (-inf; 2] и [0; 3]