** диагонали AC прямоугольника ABCD отложены равные отрезки AM и CK(точка M лежит между...

Question

На диагонали AC прямоугольника ABCD отложены равные отрезки AM и CK(точка M лежит между точками A и K). Докажите, что четырехугольник BKDM - параллелограмм, отличный от прямоугольника

Answer 1

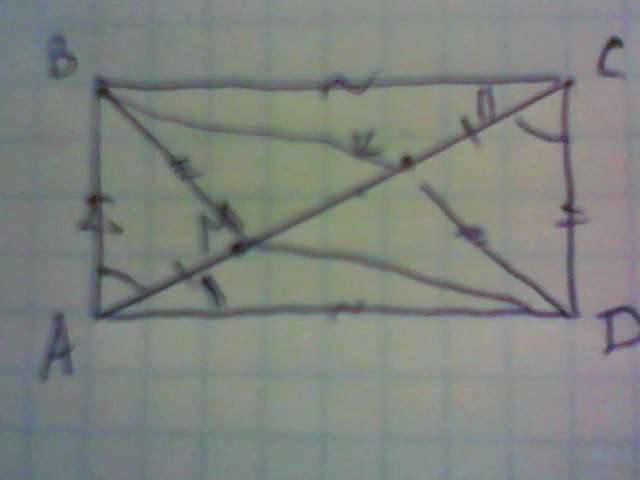
ΔАВМ=ΔСDК по двум сторонам и углу между ними. Значит ВМ=DК.
ΔАМD=ΔСКВ по двум сторонам и углу между ними. Значит МD=ВК, смотри рисунок.
ВКМD параллелограм, противоположные стороны равны.
∠ВКС+∠ВКМ=180° (смежные).
∠АМD+КМD=180° (смежные),
∠ВКМ=∠DМК, значит ВМ║DК. Этого достаточно, чтобы утверждать,
что ВКDМ- параллелограмм. 

---