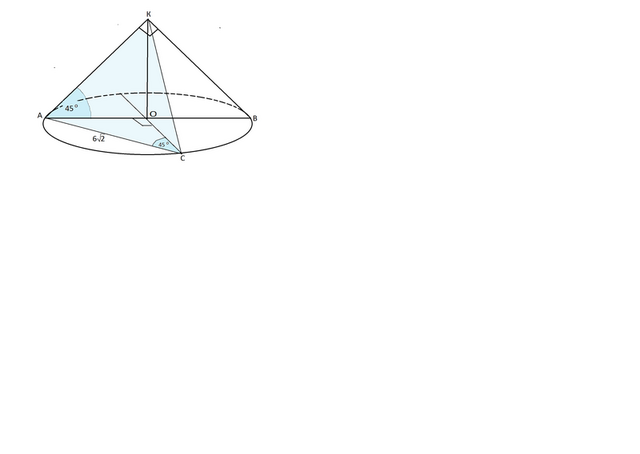
Найдите объем конуса, если хорда
его основания, равная 6√2,
отсекает четверть окружности основания,
а угол между образующей
и плоскостью основания равен 45°.
Объем конуса по классической формуле
V=1/3 S*H
Высота Н равна радиусу основания, т.к. образующая АК, АО радиус основания и высота КО составляют равнобедренный прямоугольный треугольник -
так как образующая с основанием составляет равнобедренный треугольник с углом при основании 45°.
Радиус найдем из равнобедренного прямоугольного треугольника, гипотенузой в котором данная в условии хорда - она отсекает четверть окружности, т.е дугу с центральным углом 360:4=90°.
Длина хордыАС= 6√2.
Соединив ее концы с центром окружности,
получим равнобедренный прямоугольный треугольник с катетами-радиусами основания.
Мы помним, что если гипотенуза равнобедренного прямоугольного треугольника равна а√2- катет равен а( можно проверить по т.Пифагора).
Итак, радиус конуса - 6, высота- 6.
S=πr²=π6²=36π
V=1/3·36π·6=72 (единиц объема)