Ответ:

--------------------------------------







Ответ:

-----------------------------------
График функции

в ПДСК - прямая линия, которая совпадает с осью ОХ
График функции

- прямая линия перпендикулярная оси ОХ и пересекающая ее в точке с абсциссой

.
График функции

- прямая линия перпендикулярная оси ОХ и пересекающая ее в точке с абсциссой

.
Функция

- не парная и монотонно растущая функция на всей своей области определения

функция, которая проходит через начало координат

.
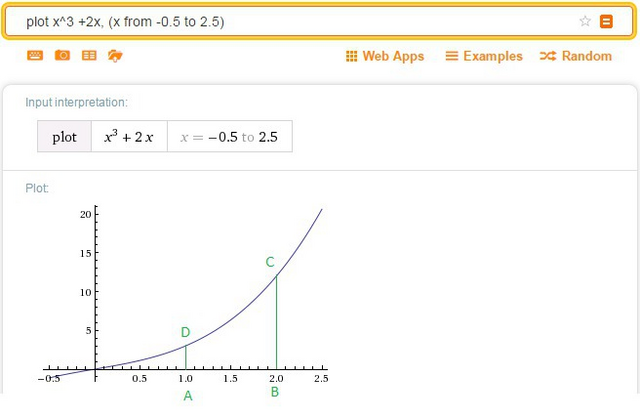
Из выше приведенного нас интересует площадь криволинейной трапеции ABCD (см. рис.).
тогда используя геометрический смысл определенного интеграла:


Ответ: