1)
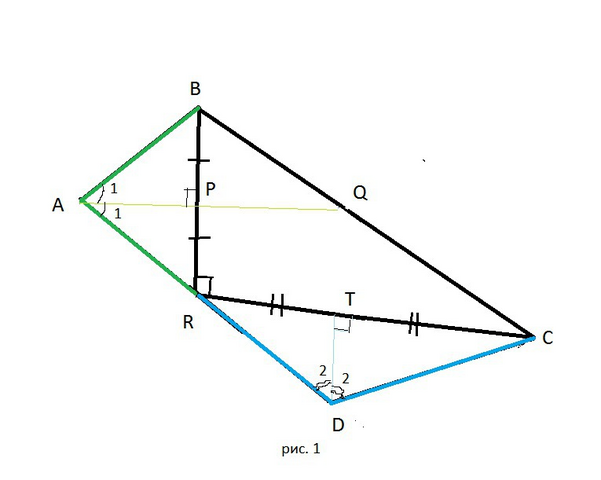
Cм. рис. 1 в приложении.
AB=AR . Δ ABR - равнобедренный, биссектриса угла А -биссектриса АР является одновременно и медианой и высотой,
ВР=РR;
АР⊥BR.
CD=DR. Δ CDR- равнобедренный, биссектриса угла D - биссектриса DT является одновременно и медианой и высотой,
RT=TC;
DT⊥RC.
Продолжим АР до пересечения с ВС в точке Q
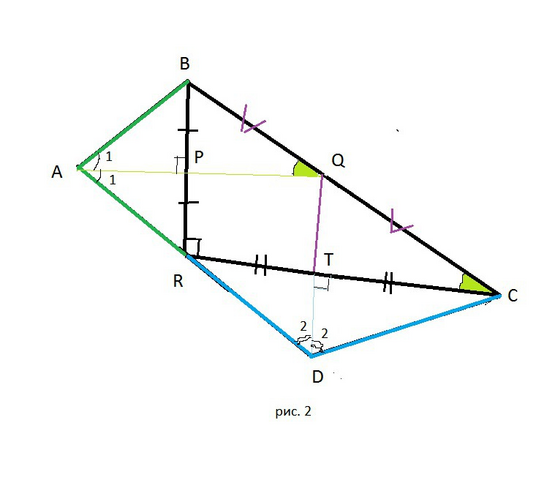
(cм. рис. 2 в приложении).
AQ ║ RC как два перпендикуляра к ВR.
Значит,
∠ВАQ = ∠BCR как соответственные при параллельных прямых AQ и RC и секущей ВС.
Δ BPQ и Δ BRC подобны по двум углам.
PQ=RC/2=RT=TC
BQ=QC
Cоединим точки Q и T.
QT - средняя линия треугольника BRC. (BQ=QC и RT=TC)
Значит QT║ BR , BR⊥ RT, значит QT⊥RT.
DT и TQ - два перпендикуляра, проведенные к RC из одной точки Т.
Значит, они совпадают.
Биссектриса DT пересекает сторону BC в точке Q.
Биссектрисы АР и DT пересекаются в точке Q, лежащей на стороне ВС.
Что и требовалось доказать.
2)
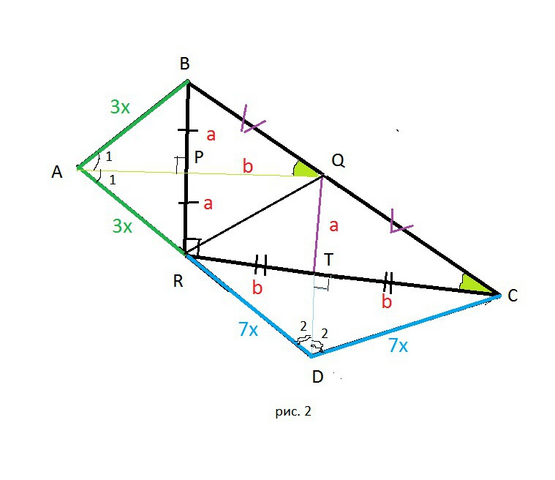
Четырехугольник RPQT - прямоугольник, три угла прямые, значит и четвертый угол - прямой.
Обозначим его стороны а и b.
Проведем диагональ RQ. Она делит прямоугольник на два равных прямоугольных треугольника RPQ и RTQ
Кроме того,
Δ ВРQ = Δ RPQ по двум катетам
Δ RTQ = Δ TQC по двум катетам.
S (Δ BRC)=2·S(RPQT)=126 кв. ед.
Δ АРR подобен Δ RTD (AP║ RT и PR║TD)
AP:RT=3:7 ⇒ AP=3b/7
PR:TD=3:7 ⇒ TD=7a/3
S (Δ ABR)=BR·AP/2=2a·(3b/7)·(1/2)=3ab/7
S (Δ RСD)=RC·TD/2=2b·(7a/3)·(1/2)=7ab/3
S( прямоугольника RPQT)=ab=63
S( ABCD)=S (Δ BRC)+S (Δ ABR)+S (Δ RСD)=126+(3ab/7)+(7ab/3)=
=126+(9+49)·63/21 =126+174=300 кв. ед.
О т в е т. S( ABCD)=300 кв. ед.