вокруг цилиндра с высотой 6 см описан шар,отрезок который соединяет центр этого шара с...

Question

Дано ответов: 2

Правильный ответ

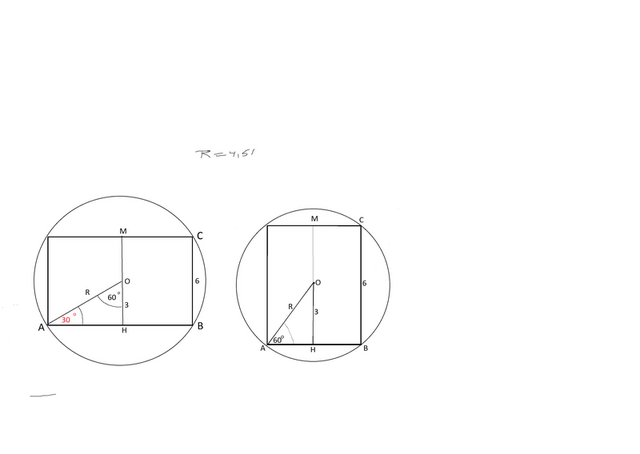
Сделаем схематический рисунок шара и цилиндра в нём.

Центр шара О,

Отрезок ОА=R и соединяет с центром шара О точку А на круге основы цилиндра.

Диаметр оснований цилиндра АВ, образующая ВС, ось цилиндра МН=ВС.

ОН = половина высоты цилиндра и равна 3 см.

Так как радиус шара образует с осью цилиндра угол 60º, то с диаметром цилиндра он

образует угол 30º

АО=ОН:sin (30º)=3:0,5=6 см

R=6 см

Sсферы= 4πr²=4π6²= 144 см²

-------------------------

-------------------------------------------------------------------------------------------------------------------------------

Для случая, когда радиус образует угол 60º не с осью цилиндра. а с его диаметром,

будет другой ответ, но ход решения, конечно, тот же.

АО=ОН:sin (60º)=3*2:√3=3*2√3:√3√3=2√3

R=2√3 см

Sсферы= 4πr²=4π(2√3)²=4π12=48π см²

Hrisula_zn (228k баллов) 11 Март, 18

PhysM_zn · Answer 1 · 2018-03-11T18:25:15+0000

Так как в шар вписан цилиндр, тогда центр шара будет делить высоту цилиндра пополам, как показано на рисунке.

Исходя из прямоугольного треугольника на рисунке, найдем длину гипотенузы численно равной радиусу сферы:

$\frac{\frac{h}{2}}{R}}=\frac{h}{2R}=cos60$

Получаем R=6

Тогда площадь поверхности шара будет равна:

$S=4\pi R^2=4\pi * 6^2=144\pi$

Ответ: $S=144\pi$