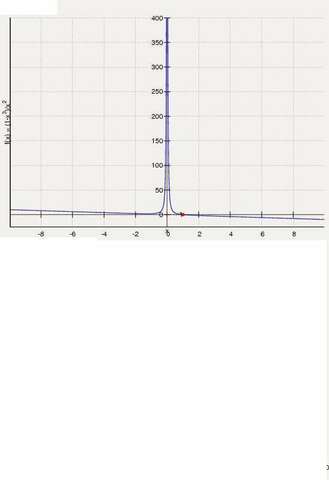
y=(1-x^3)/x^2 исследовать функцию и построить график

Question

y=(1-x^3)/x^2 исследовать функцию и построить график

Answer 1

y=(1-x^3)/x^2

1) область опр

   (-oo;0)  U (0;+oo)

2)Пересечение с осью абсцисс

   1-x^3=0

   x=1

3) функция ни нечетна и нечетна   так как х^3

4)  произв

   y'=-2(1-x^3)/x^3  -3

     -2(1-x^3)/x^3  -3=0

      -2+2x^3=3x^3

        x^3=-2

         x=-2^(1/3)

функция    убывает  (-oo; -2^(1/3)] U (0;+oo)

возрастает       (-2^(1/3);.0] 

 

 

 

 График будет симметричен оси ординат

 

 

можно наколнную асимптоту вычеслить  чтобы легче было построить

 

---

Answer 2

 

1) Обл определения:

(−∞;0)∪(0;+∞)

 

 

2) Точки пересечения с осями координат:
 x =1, точка (1,0).

 

3) не является четной, либо нечетной

 

4) точка минимума

промежуток убывания

промежуток возрастания

 

5)0 =>" alt="y''=(-\frac{x^3+2}{x^3})'=(-1-\frac{2}{x^3})'=\frac{2}{3x^2}>0 =>" align="absmiddle" class="latex-formula">  функция выпукла вниз