Формула понижения степени
cos²α=(1+cos2α)/2
Уравнение примет вид:
(1+cos4x)/2 - (1+cos6x)/2=1
cos4x-cos6x=2
Наибольшее значение, которое принимает косинус равно1
наименьшее (-1). Разность двух значений равна 2, значит
cos4x=1 ⇒ 4x=2πk, k∈Z ⇒ x=(π/2)k, k∈Z
cos6x=-1 ⇒ 6x=π+2πn, n∈Z ⇒ x=(π/6)+(π/3)n, n∈Z
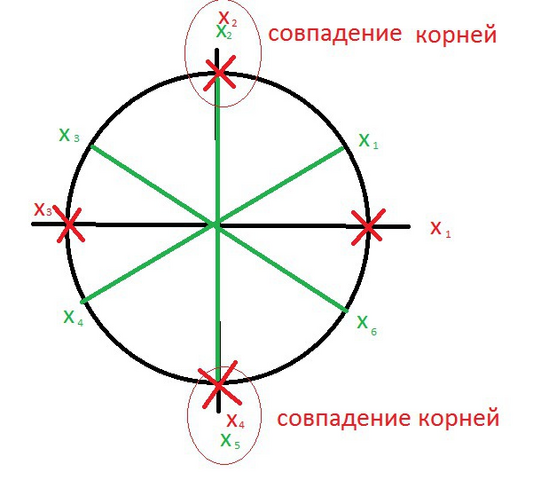
Оба условия должны выполняться одновременно, поэтому пересечением двух множеств (π/2)k, k∈Z (отмечены на рисунке красным цветом) и (π/6)+(π/3)n, n∈Z (отмечены на рисунке зеленым цветом) будут точки (π/2) + πm, m∈Z ( два совпадения на рисунке
в точках х=π/2 и х=3π/2).
О т в е т. (π/2) + πm, m∈Z.