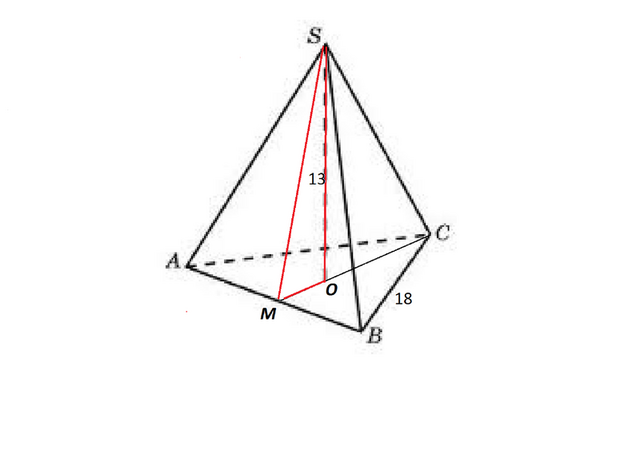
Площадь боковой поверхности пирамиды находят половиной произведения периметра основания на апофему.
Апофему SM найдем из прямоугольного треугольника, катетами в котором являются высота SO пирамиды и одна треть OM высоты CM основания
Высота основания - правильного треугольника- имеет свою формулу
h=а√3):2, где а - сторона треугольника
h=18√3):2=9√3):2 дм
Основание высоты правильной пирамиды находится в точке пересечения высот ( медиан, биссектрис) основания пирамиды - равностороннего треугольника = и отстоит от стороны основания на 1/3 длины высоты СМ.
ОМ=h:3=3√3):2 дм
SM=√(OM²+SO²)=14 дм
Sбок=3*АВ*SM:2=3*18*14:2=378 дм²