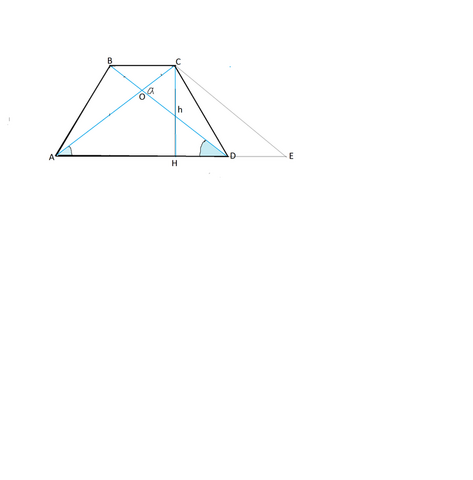
Высота равнобедренной трапеции равна h, а угол между диагоналями,
противолежащий боковой стороне, равен α. Найти площадь трапеции
Диагонали равнобокой трапеции равны, углы, образуемые при основаниях диагоналями, также равны.
Угол α - внешний угол угла АОD треугольника АОD.
Так как внешний угол равен сумме внутренних не смежных с ним углов,
то углы при основании AD равнобедренного треугольника АОD равны половине угла αкаждый.
Из вершины С трапеции проведем параллельно BD прямую СЕ до пересечения с продолжением АD.
Четырехугольник ВСED- параллелограмм, DЕ=ВС, и
АЕ равна AD+ВС, то есть сумме оснований трапеции.
Треугольник АСЕ - равнобедренный, т.к. диагонали равнобокой трапеции равны и АС=СЕ, а высота СН в нем - медиана. АЕ=2 АН
АН=СН:tg(α:2)=h:tg(α:2)
Площадь трапеции равна произведению высоты на полусумму оснований.
Полусумма оснований трапеции = АН.
Площадь треугольника АСЕ равна площади трапеции, так как АЕ= сумме ее оснований.
S трапеции равна СН·АН= h·h:tg(а:2) =h²:tg(а:2)