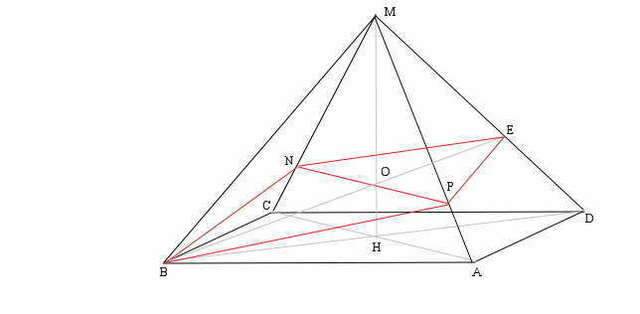
чтобы построить сечение, нужно из N провести прямую || AC
(B лежит в одной плоскости с АС)
точки N,A,C объединяет треугольник AMC
построим NP || AC в треугольнике AMC... NC=AP
BNP ---искомая плоскость... BN=BP
осталось построить пересечение с MD
т.к. треугольники NBP, MAC равнобедренные, то их высоты пересекутся в точке О
продолжим прямую BO до пересечения с MD ---точка Е четвертая вершина сечения...
NE=EP, сечение BNEP ---два равнобедренных треугольника с общим основанием...
Sсечения = S(BNP) + S(NEP) = NP*OB/2 + NP*OE/2 = (NP/2)*(OB+OE) = BE*NP/2
рассмотрим треугольник MAC, т.к. NP || AC, MAC и MNP подобны
MN / MC = 2/3 = NP / AC = MO / MH
AC ---диагональ квадрата, по т.Пифагора АС = V2 => NP = АС*2/3 = 2*V2 / 3
MH^2 = 4 - (V2/2)^2 = 4-1/2 = 7/2
MH = V14 / 2
OH = MH/3 = V14 / 6
BO^2 = OH^2 + BH^2 = 14/36 + 1/2 = 8/9
BO = 2V2 / 3
sin(OBH) = OH/OB = (V14 *3) / (6*2V2) = V7 / 4 =>
cos(OBH) = корень(1-(sin(OBH))^2) = корень(1-7/16) = 3/4
sin(MDH) = MH/MD = V14 / 4 =>
cos(MDH) = корень(1-(sin(MDH))^2) = корень(1-14/16) = V2 / 4
sin(BED) = sin(180-(OBH+MDH) = sin(OBH+MDH) =
sin(OBH)*cos(MDH) + cos(OBH)*sin(MDH) = V14 / 16 + 3V14 /16 = V14 / 4
по т.синусов BE / sin(MDH) = BD / sin(BED) и т.к. sin(MDH) = V14 / 4 = sin(BED), то
BE=BD=V2
Sсечения = V2*2*V2 / 6 = 4/6 = 2/3
(надеюсь, я нигде не ошиблась...)