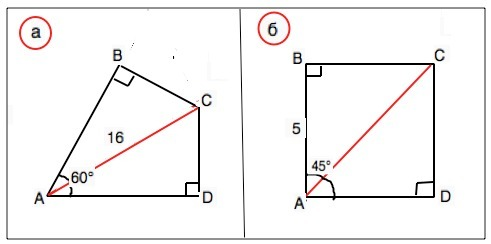
А) Сумма углов четырехугольника 360°.
Три угла известны, ⇒ угол С=360°-60°-2•90°=120°.
АС - биссектриса и делит угол А пополам.
В прямоугольных треугольниках ВАС и САD
∠ВАС и ∠САD=60°:2=30°, катеты CD и ВС противолежат этому углу. ВС=СD=АС: 2=8 см
б) В четырехугольнике АВСD биссектриса АС делит угол А пополам, и одна из этих половин=45°, значит, угол А=90°. Поэтому, поскольку углы В и D по условию прямые, четвертый угол тоже равен 90°, а так как угол ВАС=45°, то ∆ АВС и ∆ САD - равнобедренные. Поэтому ВС=АВ=СD=5 см