F(x) = |cos x|,
g(a,x) = x^2 + a,
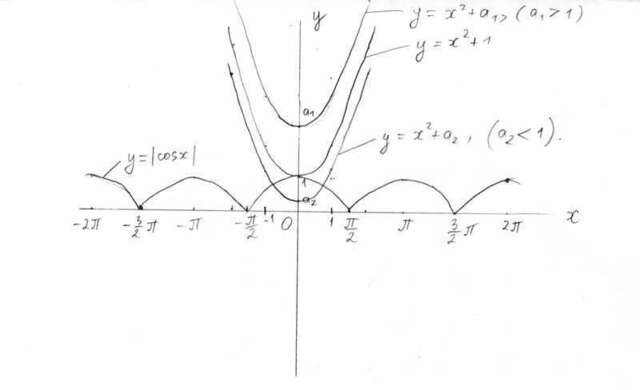
g(a,x) - это семейство парабол (в зависимости от параметра а).
и уравнение сводится к следующему
f(x) = g(a,x),
f(x)<=1, для любого икс.<br>При a>1, g(a,x) = x^2 + a>1, и в этом случае (a>1) решений нет.
При a = 1, g(a,x) = g(1,x) = x^2 + 1 >=1, для всех икс.
|cos x| = 1, и x^2+1 = 1, <=> x=0, (т.к. |cos 0| = 1).
Таким образом, a=1, это часть ответа.
При а<1, будет два корня, это видно по графику (см. приложение).<br>Ответ. a=1, x=0.