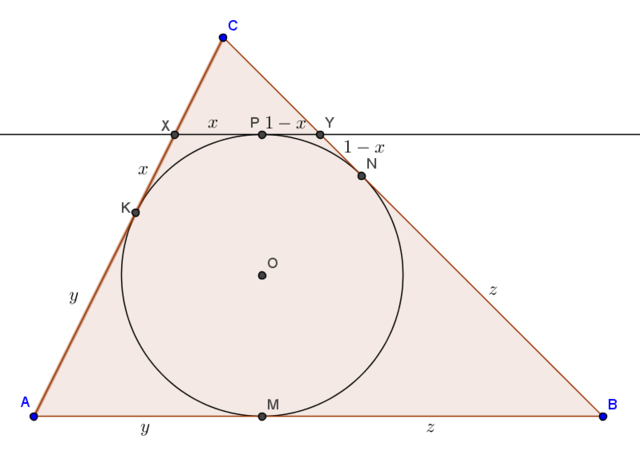
Обозначения смотрите на рисунке, использовано то, что отрезки касательной, проведенных из одной точки, равны.
Прямая ХY параллельна AB, тогда треугольник XYC подобен треугольнику ABC (хотя бы потому, что равны соответственные углы).
Тогда AC/CX = CB/CY = AB/XY = y+z
Найдем длину СХ.
(AX+CX)/CX=y+z
AX/CX+1=y+z
CX=AX/(y+z-1)=(x+y)/(y+z-1)
Аналогично, CY=(1-x+z)/(y+z-1)
Периметр треугольника, таким образом, равен
P=AX+XC+CY+YB+BM+MA=y+x+(x+y)/(y+z-1)+(1-x+z)/(y+z-1)+1-x+z+z+y
P=2(y+z)^2/(y+z-1)
Итак, периметр равен P=2AB^2/(AB-1)=8
2AB^2=8AB-8
AB^2-4AB+4=0
AB=2
Ответ. AB=2.