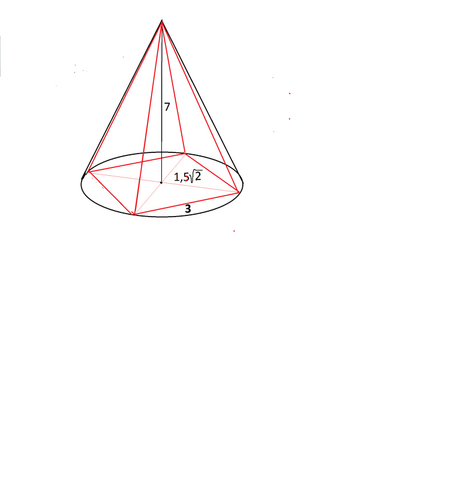
Высота конуса совпадает с высотой пирамиды.
Диаметр основания конуса равен диагонали квадрата - основания пирамиды, т.к. квадрат этот вписан в основание конуса.
Диагональ квадрата равна а√2, а квадрата со стороной 3 равна 3√2
Радиус r конуса равен половине диаметра и равен 1,5√2
По формуле
V=πr²H:3 найдем объем конуса
V=π(1,5√2 )²H:3=π4,5*7:3=10,5π
Объем, деленный на π, равен 10,5