Два уравнения считаются равносильными, если множества их решений совпадают, равны друг другу.
Пара: 
и 
уравнение равносильно уравнению 
, множеством решений которого есть единственное число, а именно: 
, при подстановке в уравнение этого числа уравнение превращается в верное числовое тождество, а именно 
уравнение равносильно уравнению 
среди действительных чисел мы не найдем такого числа, которое превратит это уравнение в верное числовое тождество, по скольку при 
из множества действительных чисел выполняется следующее неравенство: 
.
Т.е. никак 
не может равняться отрицательному числу, и 
в том числе.
Ответ: не равносильны
-------------------------------------
Пара: 
и 
аналогично к анализу предыдущей пары уравнение не имеет решений на множестве действительных чисел.
уравнение равносильно уравнению 
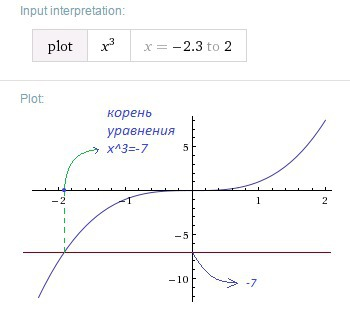
функция 
монотонно растет (при увеличение аргумента функции, ее значения функции только увеличивается) на множестве своего определения, т.е. на всем множестве действительных чисел
график функции 
- проведенная через точку 
параллельно оси ОХ прямая линия.
Т.е. графики функций и пересекаются в одной точке, и эта точка пересечения графиков отвечает единственному действительному решению уравнения
Т.е. множества решений снова не совпали
Ответ: не равносильны
